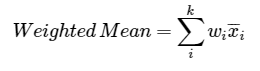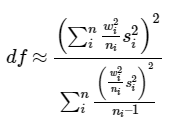Data Quality Evaluation
This section will demonstrate how to determine if ISM data are sufficient and will also provide guidance on using appropriate statistical methods for data evaluation and confident decision-making.
6.1 Data Verification, Validation, and Usability
As mentioned in previous sections, careful planning is needed prior to using an ISM sampling design, and part of that planning should include how the ISM data will be evaluated relative to the intended use as defined in the DQOs. This evaluation should include verification, validation, and an assessment of the final usability relative to the defined study questions. Users are referred to UFP-QAPP worksheets for details on planning and documenting these data evaluation steps (USEPA 2005).
As part of the data evaluation process, the project team should consider what inputs will be used during data verification, data validation, and DUAs. Inputs might include but should not be limited to field records, interim reports and final reports of analyses (including QC results from milling blanks, surrogates, and spike recoveries), replicate results, and further data validation reports. Inputs for data evaluation should document the procedures that will be used to verify and validate project data, including the specific requirements/specification, who is responsible for performing each activity, and how they will be documented.
6.1.1 Data verification
Data verification is a completeness check that all specified activities involved in data collection and processing have been completed and documented and that the necessary records (objective evidence) are available to proceed to data validation. This includes the need to ensure that the sampling plan was properly designed and that the samples were properly collected in the field and processed for testing at the laboratory. For example, if the ISM sampling design called for 30 increments to be collected in each DU but only 25 were taken, this would be documented during the data verification evaluation.
6.1.2 Data validation
The quality of the sample data generated must be reviewed to determine if the data are reliable to answer the risk and/or remediation-based questions prepared at the beginning of the project. This requires a review of the sampling plan design and the methods used to collect the samples.
Data validation is an analyte- and sample-specific process for assessing conformance to stated requirements, methods/SOPs, and specific performance criteria. The scope of data validation needs to be defined during project planning because it affects the type and level of documentation required for both field and laboratory activities. If data validation procedures are contained in an SOP or other document, the procedures should be referenced or included as an attachment to the QAPPs.
Data validation includes confirming the qualifiers assigned to results, with any data qualifiers applied by the data validator clearly defined. Common data qualifiers include estimated values (such as J flags), which is when results are greater than an MDL and less than a method RL (MRL), and non-detects (such as U flags), which is when results are less than an MDL. For ISM datasets that include one or more non-detects (such as censored data), there is greater uncertainty in parameter estimates, including 95% UCL calculations. At this time, numerical simulations used to support the recommendations in this report regarding statistical analysis methods for ISM data (see Section 3.2) are based on datasets that are not censored, so there is uncertainty in applying the same methods to censored data.
Many methods exist for parameter estimation for censored data, and although their computations are no different for ISM data than for any other environmental dataset, caution must be used when sample sizes are small. EPA provides guidance statistical analysis with censored data based on minimum sample sizes of 8 to 10 observations, of which at least five are detects. EPA notes that Kaplan-Meier (KM) estimation has been shown to yield more reliable estimates of the AM and SD than imputation (that is, substitution) methods such as MDL, MDL/2, and under these conditions. However, for ISM datasets with small sample sizes (<5 detects) even KM methods are likely to yield very high uncertainty in parameter estimates. Therefore, it may be advisable to explore both imputation and KM methods as a form of uncertainty analysis, particularly if the MDL is close to a relevant AL (within one SD).
Data validation should also note that when performance criteria are not met, such as failing to meet QC recoveries for surrogates or spikes. Note that final rejection of any data and their use is a decision reserved specifically for the project team and will be made during the DUA.
6.1.3 Data usability
The DUA is performed by key members of the project team, as defined during the SPP at the conclusion of data collection activities. The DUA should be integrated into the definable features of work where decision-making occurs. For phased investigations, the DUA and decision-making will occur at each phase. Table 6-1 summarizes the recommended steps of a DUA.
- Summarize lessons learned and make recommendations for changes to the DQOs or the sampling design for the next phase of investigation or future investigations if needed.
- Prepare the data usability summary report.
Table 6-1. Recommended steps for a DUA.
Source: ITRC ISM Update Team, 2020.
| Step 1 | Review project objectives and sampling design.
|
| Step 2 | Review the data verification/validation outputs and evaluate conformance to performance criteria.
|
| Step 3 | Document data usability, update the CSM, apply decision rules, and draw conclusions.
|
| Step 4 | Document lessons learned and make recommendations.
|
The DUA involves a qualitative and quantitative evaluation of environmental data to determine if the project data are of the right type, quality, and quantity to support the measurement performance criteria (MPC) and DQOs specific to the investigation. It involves a retrospective review of the SPP and the CSM in order to evaluate whether underlying assumptions are supported, sources of uncertainty have been managed appropriately, data are representative of the population of interest, and the results can be used as intended with an acceptable level of confidence. The DUA is a retrospective evaluation of all aspects of the data and project investigation to determine whether the data support their intended uses. Therefore, the DUA represents a critical step in determining if final decisions can be made as stipulated in the DQOs.
A summary matrix of each topic is provided in Table 6-2. The table is not intended to be comprehensive for all aspects of the investigation and should be modified as appropriate on a site-specific basis. Refer to the noted sections of this guidance document and related appendices for detailed information on each topic. Deviations from the recommended methods should be discussed in the investigation report and resulting limitations of the data collected, described, and considered in the report’s recommendations. Methods to help minimize data error when the sample collection and analysis conditions noted in Table 6-2 cannot be met are discussed in the associated appendices.
Table 6-2. Sample data quality and usability matrix.
Source: ITRC ISM Update Team, 2020..
| Acceptable? | Site Investigation Stage |
| CSM and DU Designation (see Section 3.1) | |
| Site history and potential sources and type of contamination well understood? | |
| Site investigation questions used to designate DUs for testing clearly stated and based on risk and/or optimization of anticipated remediation requirements? | |
| Questions and decision statements developed for individual DUs presented? | |
| Area and total volume of soil associated with each DU noted and acceptable for intended purposes? | |
| To-scale map depicting location and size of DUs provided? | |
| Field Sample Collection (see Section 4) | |
| Summary of sample collection methods provided, including approximate final mass of each sample? | |
| ISM samples prepared by collecting and combining a minimum of increments appropriate for the chemical present and nature of contamination? | |
| Increments appropriately spaced and collected? | |
| Complete, unobstructed access to all portions of the DU soil available for sample collection? | |
| Increments collected over a uniform depth and without biasing soil size? | |
| Samples to be tested for volatile chemicals preserved in methanol in the field or met requirements for alternative preservation and testing methods? | |
| Minimum sample mass of 1 kg met (minimum 300-g for samples to be tested for volatile contaminants)? | |
| Three replicate ISM samples collected appropriately to test total data precision or calculate CIs? | |
| Laboratory Processing and Testing (see Section 5) | |
| Samples to be tested for non-volatile chemicals air-dried and sieved to target particle size for each specific DU? | |
| Analytical subsample collected using a sectorial splitter or manually collected from at least 30 points? | |
| Minimum 30-g analytical subsample mass extracted for <2-mm particle size soil? | |
| Minimum 10-g analytical subsample mass extracted for <250-µm particle size soil? | |
| Three replicate analytical subsamples collected from at least 10% of samples submitted (minimum one set)? | |
| Holding times met? | |
| Analytical QC and QA criteria met (spikes, blanks, and so on, refer also to USEPA 2002)? | |
| Replicate Sample Collection and Data Precision Evaluation | |
| Replicate field sample and laboratory subsample data meet data precision requirements? | |
| Source of error determined for replicate data that exceed the RSD identified as problematic during planning? | |
| Laboratory subsampling error identified and subsamples recollected after grinding of primary sample or larger subsample mass collected? | |
| Data adjusted or new samples collected for DUs with replicate data that exceed the RSD specified as unacceptable during planning? | |
6.2 Evaluation of DU Results
As in discrete sampling, there is no one decision mechanism dictated by the use of ISM sampling – a variety of decision mechanisms are possible. Each decision mechanism has strengths, weaknesses, and assumptions. In some cases, agency requirements will dictate the approach to be used, but in others, a consensus on the decision mechanisms to be employed needs to be reached among members of the planning team prior to finalization of the sampling plan. Because ISM yields estimates of mean concentrations within a DU, it is important to note the spatial and/or temporal scale that was originally intended in the development of the AL.
6.2.1 Evaluation of DU results
This section provides three examples of decision mechanisms and how to evaluate ISM data. The DQOs may specify that DU results are either used in risk assessment or compared with ALs, which may consist of regulatory screening values, threshold values derived from risk assessment, or other regulatory values.
6.2.1.1 Single DU sample result
The simplest decision mechanism is the comparison of a single ISM sample result for a DU to an AL. Sometimes, more than one set of ALs may apply to a site because they reflect different objectives (human health or ecological endpoints, leaching and groundwater protection, short-term risk, and so on). This decision mechanism is simple, straightforward, and the most cost-effective, since only one ISM sample is collected. The result of the decision is immediately apparent, too – a failure is indicated if the ISM sample result exceeds the AL.
A single ISM sample provides one estimate of the mean concentration, so the practitioner must be aware of the inherent limitations when using a single ISM result in regard to potential uncertainty with the comparison. Single ISM results do not allow for the calculation of a DU-specific CI or quantification of the precision of the estimate. As a result, it is difficult to predict how far from the actual mean a single ISM sample result might be. Use of a single ISM result might be acceptable when the estimated mean concentration obtained is much greater than (or much less than) the AL such that even a great deal of error in the mean estimate could be tolerated without making a decision error. Note that predetermination of the “much greater than” or “much less than” values should be addressed during the site planning process. In this situation, the ISM sample may provide confirmation of what may have already been strongly suspected – that the DU clearly passes or fails.
These decisions are site-specific and cannot be outlined in a guidance document, but there is consensus that the uncertainty about making the right decision increases as the ISM sample result gets closer to the AL.
The uncertainty of a single ISM sample result may be reduced if numerous single ISM sample results are evaluated, assuming all DUs fall within the same CSM and site assumptions. For example, if 10 single ISM results are all considered comparable, it is unlikely that all of the results either under- or overestimated the actual mean concentration.
6.2.1.2 Mean of replicate DU data
In this decision mechanism, replicate ISM samples are collected in the field from the same DU and provide a measure of the variability of the entire sampling, preparation, and analytical process. The mean concentration of the replicates is calculated and compared to the AL and is likely to be closer to the true mean of the DU than the result from a single ISM sample, therefore, it can be considered to provide a more reliable estimate of the mean. Because a CI has not been calculated, though, there is no assurance that the actual mean concentration has not been under- or overestimated, so this decision mechanism cannot be used for projects requiring the calculation of a CI, such as a 95% UCL.
6.2.1.3 95% UCLs, CIs on the mean of replicate DU data
In this decision mechanism, replicate ISM samples are collected in the field from the same DU as in the previous example, except that a CI may be calculated and applied to the mean concentration. The 95% UCL is commonly selected as an EPC, which can be calculated based on the measured RSD from the replicates. Use of a 95% UCL improves the confidence associated with comparing the ISM results to the ALs. It provides protection against underestimation, but it may also overestimate the true mean concentration.
Project objectives may specify that the estimate of the mean concentration provided by ISM sampling must be health protective, meaning that there is a low chance of underestimating the actual mean concentration within the DU, which is achieved by calculating the 95% UCL. It is important to recognize that the likelihood of underestimating the mean from any sampling method (discrete, composite, or ISM) increases as the degree of heterogeneity increases.
For those accustomed to working with 95% UCL values from discrete datasets, there are some important differences with ISM data. Discrete sampling designs generally require more samples than ISM designs because of the greater variability and reduction in site coverage. A 95% UCL for ISM data may be calculated with as few as three ISM samples (see Section 3.2.4). Additional ISM replicates increase the performance of the mean estimate (providing a 95% UCL closer to the actual mean), and although this increases the cost, it may be worthwhile if the site is relatively large or heterogeneous, and the result is anticipated to be close to the AL.
A second difference involves what to do if the 95% UCL is higher than any of the individual values used in its calculation. With discrete datasets, the maximum concentration observed is often used if it is less than the calculated 95% UCL (though the sample maximum will not necessarily be a conservative estimate of the population mean). With ISM data, the calculated 95% UCL value should be used even if it is higher than any of the individual ISM results. This situation is common when three replicate ISM samples are collected because the 95% UCL always exceeds the highest individual ISM result. Two methods for calculating the 95% UCL from ISM data are available for any ISM design: Student’s-t and Chebyshev. For designs with at least seven ISM results for each DU, bootstrap methods may also be used. Bootstrap 95% UCLs often result in a more accurate estimate of the true mean than Chebyshev, but coverage may be reduced slightly below 95% (see Appendix B). As discussed in Section 6.3.2, the choice of method depends on the known or anticipated shape of the PD of contaminant concentrations in the DU. Note that software programs for calculating 95% UCL values for discrete sample data (such as ProUCL) contain algorithms optimized to perform well for discrete data only, thus, they are generally unsuitable for calculating 95% UCL values for ISM data. An ISM 95% UCL calculator for deriving 95% UCL values for ISM data is presented in Section 3.2.4.1.
6.2.2 Weighted means and 95% UCLs from multiple SU or DU results
Projects may require combining several SUs into a DU or perhaps determining multiple DUs to make a site decision. There are two types of instances where this might occur:
- A site has areas with different conceptual models in terms of expected contamination, as could happen when there is, for example, a stream channel, a meadow, and a rocky out-cropping in an area that we would like to define as an EU. Each of these areas might be investigated as a separate SU or DU for site characterization but then combined to define a single EU.
- A site with multiple ecological exposures would consider a variety of sizes of DUs to accommodate multiple receptor scenarios. If, for example, the area of a pocket mouse habitat is a quarter that of a muskrat, which is an eighth of that of an eagle, then we might need to sample in DUs of a size defined for pocket mice but then combine DUs for the receptors with larger home ranges.
When DUs need to be combined, the variable sizes of each can be taken into account by using a weighted mean. (In this context, statisticians often refer to the smaller DUs or SUs as strata.) Depending on project needs, a weighted 95% UCL could also be calculated.
Table 6-3 provides a numerical example of this calculation where data from two DUs are combined to derive a 95% UCL for a larger DU (α = 0.05). In this example, an elementary school is divided into two DUs representing different play areas: DU1 is the kindergarten playground, and DU2 is the playground for older children. A maintenance worker has contact with both DUs, and a separate DU is constructed to reflect exposure of this worker. Assume the concentrations of replicate results in DU1 and DU2 are as in the table, based on n = 30 increments per replicate.
Table 6-3. Summary statistics used to combine DUs.
Source: ITRC ISM Update Team, 2020.
| Playground Area | Area (Acres) | Sample Statistics | 95% UCL | ||
| Replicates | Mean | Chebyshev | Student’s-t | ||
| DU1 (Kindergarten) | 0.25 | 120, 100, 140 | 120 | 170 | 154 |
| DU2 (Older Children) | 1.0 | 22, 25, 30 | 25.7 | 35.8 | 32.5 |
| Equal Weight | 1.25 | 120, 100, 140, 22, 25, 30 | 72.8 | 168 | 117 |
| Proportionately Weighted | 1.25 | 120, 100, 140, 22, 25, 30 | 44.5 | 57.5 | 50.9 |
If it is assumed that, on average, a maintenance worker spends equal time in DU1 and DU2, then the replicates from each DU can be weighted equally, yielding the results shown in the third row of Table 6-3. Alternatively, it may be assumed that a maintenance worker’s exposure is proportional to the respective areas of each DU, and can be used to generate summary statistics for the combined area. Note that by proportionately weighting the DUs by area, the results are considerably different than if the area was not taken into account for the combined area shown in the last row of Table 6-3. The weighting factors applied to each DU should sum to 1.0, which is achieved by dividing each area by the combined acreage of 1.25:
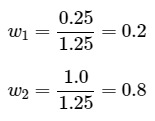
Download the calculator for the weighted 95% UCL for a combined DU from several smaller DUs (see ISM 95% UCL calculator) from Section 3.2.4.1.
This same methodology can be used to combine a surface DU with its corresponding subsurface DU. The only slight difference would be that the weight term would reflect the proportion of the total soil volume within the DU. For designs with at least seven ISM results, weights could be incorporated into a bootstrap methodology by resampling ISM results with unequal probabilities, in proportion with the desired weights. For more details on bootstrap methodology, see, “The statistical sleuth: a course in methods of data analysis” (Ramsey and Schafer 2012).
6.2.3 95% UCL from multiple SUs or DUs provides spatial distinctions
When replicate samples are collected over the entire DU, each single ISM sample (or singlet) result provides a separate estimate of the mean concentration, and these estimates can then be combined to derive a 95% UCL as discussed in Section 6.2.1.3. Another approach is to divide the DU into SUs and collect one ISM sample from each SU. The results from each ISM sample (that is, each SU) can also be combined to calculate a 95% UCL for the DU. With the latter approach, the ISM samples are not true replicates of the mean throughout the DU in the sense that they provide information on different portions of the DU. Collectively, however, they can provide an unbiased estimate of the mean. Combining singlet SUs or DUs does not provide information about the variability within the singlet if replicates are not available.
The principal disadvantage to this approach is that the 95% UCL often exceeds the true mean by a larger degree than if replicates had been collected across the entire DU. Another disadvantage to combining singlet ISM SUs or DUs is there is no measure of variability within the SU or individual DU when data from replicates are not available. The principal advantage of subdividing the DU for this decision mechanism is that it provides some information on the spatial distribution of contamination. If the DU as a whole fails the comparison with the AL, this spatial information could be valuable if a decision is made to break the DU into smaller DUs for reevaluation.
For example, the DU in Figure 6-1 displays a 95% UCL ISM concentration (calculated based on three replicates) that exceeds the AL of 4.0 (Figure 6-1A). Because spatial information is not available to help determine where in the DU the AL is exceeded, the entire DU is considered to be in exceedance. To obtain spatial information on the contaminants, the DU is divided into smaller SUs based on the CSM, and a 95% UCL calculated from three replicates for each SU (Figure 6-1B). This spatial information shows that only a portion of the DU exceeds the AL.
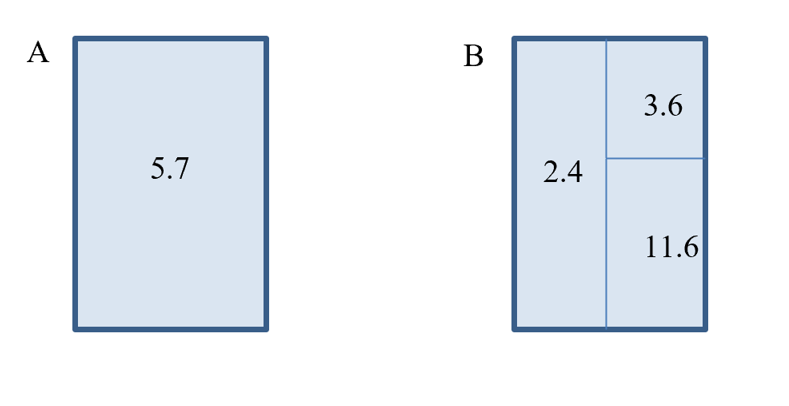
Source: ITRC ISM Update Team, 2020
As noted above, a disadvantage of using a weighted 95% UCL calculated when a DU is divided into smaller SUs is that it may exceed the 95% UCL produced when increments were collected across the DU. For this example, the area with a 95% UCL of 2.4 is 40% of the DU, the area with a 95% UCL of 3.6 is 20% of the DU, and the area with a 95% UCL of 11.6 is 40% of the DU. Using the weighted means equations from earlier results in a DU 95% UCL of 6.3, which is larger than the 95% UCL of 5.7 that was obtained from the entire DU. Therefore, the decision to divide DUs into smaller SUs will depend on the possible distribution of contaminants at the site and whether concentrations are expected to be relatively homogenous or vary greatly with location. If similar variation is expected across the SUs, an alternative option involves collecting one of the SU or DUs in replicate, applying the measured RSD to each of the SU or DU results, and proceeding with the weighted 95% UCL calculation discussed above. Assuming that the CSM predicts or presumes that the heterogeneity within the measured replicates is applicable to the remaining SU or DUs, this option eliminates the overestimation of the 95% UCL. Section 3.3.2 gives additional details on various possibilities to structure the statistical analysis of DUs with smaller SUs.
6.2.4 Differences between discrete and ISM 95% UCLs
Both ISM and discrete sampling represent a mean concentration for a volume of soil, with discrete samples representing the mean concentration in the volume of soil removed for a single grab sample. This concentration (by itself) does not provide any information about the mean concentration of the DU. Because discrete samples represent only a small volume of soil, multiple discrete samples are needed to estimate an average concentration for the DU. ISM samples are structured composite samples that, when taken correctly, provide an estimate of the mean concentration for the entire DU. Although 95% UCLs can be computed from both discrete and ISM datasets, the two methodologies would produce very different distributions when applied to the same DU (see Section 2.4.1 and Figure 2.8). This is because they represent different properties of the population that is sampled in the DU. While the arithmetic mean of the populations represented by the sampling distributions is the same, the resulting sampling distributions will not be. Efforts to adjust the data and/or summary statistics so that the distributions match are unlikely to fully address the key factors that contribute to their differences (such as differences in sample support and laboratory procedures).
6.2.5 Use of discrete historical data
Discrete sample results (representing individual site measurements) are not directly comparable to ISM sample results, which represent mean estimates, so resampling the discrete data to simulate hypothetical ISM results will not address the disparity between discrete and ISM sampling protocols. Resampling merely provides a means of generating statistics for “composite discrete” samples rather than structured composite ISM samples. Since each ISM sample is a representative mean concentration, the SD of the ISM replicates is similar to the SE. Stated in mathematical terms, the proposed approach is similar in concept to dividing the sample SD (from discrete sampling) by the square root of the sample size n in order to approximate the SD of the ISM replicates (that is, the SE of the population). Because the variability of ISM replicates is an estimate of the variability in mean concentrations, it is similar to a SE, as it includes variability within field and laboratory measurements. Great care must be applied to understanding hypothetical ISM results as they may be biased high as a result of using the underlying discrete samples and could introduce new decision errors. For example, variability associated with the original discrete samples associated with sample mass may not have been quantified and may not be comparable to the mass of sample collected through an ISM sample.
This is a major limitation in the proposed approaches for mixing simulated ISM results (from historical discrete sampling) with real ISM results and casts doubt on the reliability of the approach for regulatory decision-making.
6.2.6 Mixtures of discrete and ISM data
There are no established methods for combining discrete and ISM data, but ISM and discrete data can both help inform decision-making at the site. Either sampling methodology can be used for site characterization, delineation, confirmation sampling, and comparison to background, although the type of sampling used may vary depending on project goals, size of the site, funding, and other variables. The use of both ISM and discrete data at a site often provides a more complete picture of the nature and extent of contamination than either sampling method alone. For example, historical discrete sampling may be used to inform the delineation of SUs at a site, and because heterogeneity is higher with discrete data, ISM can then be used to obtain a better estimate of the mean concentration across the site. Although these two types of sampling are complementary, they are not equivalent. If combining discrete and ISM samples is deemed absolutely necessary, it should be done carefully and with the help of a trained statistician familiar with ISM site investigation methods.
6.3 Evaluation of Statistical Assumptions
Due to the low sample sizes typical of ISM sampling, many statistical tests designed to evaluate whether data meet assumptions may not be appropriate or may have low power to draw conclusions. A statistician should be consulted to evaluate the appropriateness of various tests.
After identifying the desired method of statistical analysis, it is important to check the assumptions of that method before analyzing data. Common assumptions include independence and normality in the data, and unbiased samples collected using a valid statistical design. Statistical sampling should be addressed in the sampling design in Section 3. The placement of the increments within an ISM sample should generally be selected randomly, but if there are more SUs that need to be sampled, the selection of those SUs should also be done randomly.
6.3.1 Independence
Most analytical methods will require field replicates to be independent – in other words, the value of one ISM result in a particular DU should not have any effect on ISM results in the same DU. Due to the nature of ISM in that increments are collected spatially across the entire volume or surface area, spatial trends within an SU should not cause a violation of the assumption of independence. This is because each composite has more spatial coverage than a discrete sample and has the potential to cover both high and low-concentration areas within a particular SU with a spatial trend.
In the case where a DU consists of more than one SU, the evaluation of spatial scale as it relates to independence of field replicates becomes more complicated. ISM requires the assumption that the SUs are exchangeable in order to meet the assumption of independence. Consider the case of a DU consisting of four SUs. If there is a spatial trend across SUs such that some SUs are more similar to each other than others, then ISM samples collected from each SU would not be exchangeable from one another, and the independence assumption would be violated. The consequence is that the variation will be underestimated. In this case, the groups of SUs that are exchangeable should be analyzed separately and only combined in an additional step to obtain the results for the entire DU (see the example in Section 2.5.3). If, however, a DU is divided into four equally-sized SUs, and each SU is separately sampled, a reasonable estimate of the DU mean should be obtained.
Another common assumption in analytical methods is that laboratory replicates are independent from one another. It is important that, in sample processing, the sample is as homogeneous as possible, such that each subsample in the volume of soil can be assumed to be exchangeable. Refer to Section 5 for a discussion of sample processing.
6.3.2 Normality
Another assumption of many commonly used methods is that the data are normally distributed. The CLT states that the distribution of the mean is normally distributed (see Section 3.2.5), but in ISM, physical averaging based on increased sample volume is done instead of statistical averaging. In cases of extremely skewed datasets, such as extremely variable PCB or dioxin contamination, the CLT may not apply, but it should apply to the majority of ISM datasets. Because of small sample sizes in ISM data, a formal or statistical evaluation of normality can be difficult, so conceptual knowledge of the site can often be helpful. In general, unless there is a reason to suggest highly skewed data, the assumption of normality is probably appropriate, as shown in Section 3.2, Figure 3-17.
In cases with sufficient sample sizes, the best way to evaluate the assumption of normality is to simply look at the data visually, such as with a histogram. Many researchers recommend formally testing for normality (the Shapiro-Wilk test is an option), but this is problematic with fewer than eight samples. These tests require evidence to reject normality, rather than evidence to confirm normality. ISM data usually will not have sufficient samples to reject normality regardless of the true distributional form. If such tests are used, they should be only part of a larger evaluation of normality that also includes visualizations and conceptual knowledge.
Although assumptions of particular methods should always be checked, it is often difficult to be truly confident that they are met, particularly when it comes to normality of small datasets. Fortunately, most methods (such as the 95% t-UCL and Chebyshev 95% UCL) are robust to small deviations in normality, meaning these methods are still effective and provide the desired level of coverage and accuracy, even if the data are not quite normal.
In studies comparing ISM samples from one site to another, or a site to background, there is often the additional assumption of equal variance in ISM results – in other words, the spread of the values obtained from each site should be similar. Much like the assumption of normality, this can only be evaluated with sufficient sample sizes. For the small sample sizes typical of ISM sampling, reasonable professional judgment and site knowledge may be used to determine whether there is a reason for differences in variance between two sites or datasets. For larger sample sizes (typically at least seven or eight), the assumption of equal variances is best evaluated by visually comparing the data using figures such as histograms or boxplots. In addition, the estimates for SD between site and background datasets may be compared. A formal test for equal variance can be conducted (such as Levene’s test), but sample sizes for ISM data are rarely large enough to make a conclusive determination on whether the assumption is met. In reality, site concentrations are expected to be more variable than background concentrations if contamination exists. Common background tests such as the two-sample t-test are robust to mild deviations from homogeneity of variances, but for severe differences in variances, other statistical tests may be implemented, such as Permutation tests.
6.4 Decision Endpoints
Each project and corresponding CSM and DQOs will determine the intended data use. Data quality needs for decision-making should be carefully planned by the project team and documented in the planning documents, which should also provide the “if-then” alternatives to be taken in the event that project QC goals are not met. This is particularly critical for complex and/or large-scale ISM projects such as those commonly seen.
Initially, the DQOs should provide the overall structure for data evaluation and use – for example, if the purpose of the DUs is to determine if a specific chemical was over an AL.
In many cases, changes to the CSM or unanticipated larger-scale trends may be detected. In addition to straight comparisons of results to ALs, for instance, larger trends in chemical concentration gradients may become apparent that were not part of the DQO design.
6.4.1 Step 1: initial DU data evaluation
The initial evaluation should begin by evaluating the raw/parent results, that is, ISM sample values. Before conducting detailed reviews, replicate reviews, or statistics, begin with simple, large-scale evaluations that focus on answering the following questions:
- Do the concentrations meet the anticipated CSM? For example, are ISM values in the anticipated range?
- Did the laboratory detection limits meet the sensitivity needs documented in the DQOs? Are the data usable for the intended purpose?
- Does it appear there are anomalies or outliers? For example, are there contiguous DUs with very different concentrations or combinations of concentrations not anticipated relative to the CSM?
- Was information not previously anticipated now present? For example, during field sampling, were there any new observations about soil types? Were some DUs not sampled because of obstacles or other physical limitations?
This initial evaluation can help determine if the overall objectives were met, or if the project would benefit from splitting existing DUs into smaller DUs in a subsequent sampling event to better understand chemical variability. Several examples of data comparison scenarios are provided in Sections 2.5.3 and 6.2.1.
6.4.2 Step 2: detailed evaluation of ISM results, replicate data and action levels, and CIs
Following the initial evaluation, each project will have its own objectives in terms of detailed evaluation of the results. Examples of the different types of possible detailed evaluation/data use include the following:
- comparison of a summary statistic (single ISM estimate of the mean, the mean of multiple ISM results, the 95% UCL of multiple results, and so on) to an AL
- comparison of results of a quantitative risk assessment that used a summary statistic (commonly a 95% UCL) to an acceptable risk range for carcinogens (such as a 1 × 10-6 excess cancer risk to 1 × 10-5 excess cancer risk) or to an acceptable hazard threshold for noncarcinogens
- comparison of site and background datasets
- combination of data across multiple DUs
- extrapolation of statistics across DUs
Statistical evaluations of field replicate results are used to determine how well the ISM sampling protocol captures the spatial heterogeneity of the contaminant distribution (Table 3-3). Project planning steps should thus include specific metrics to evaluate the acceptable RSD, CIs, or other evaluating factors to be applied to field replicates. The following provides an example of how to evaluate CIs as an example of field replicate evaluation and confidence in decision-making, as demonstrated in Figure 6-2:
- If the parent concentrations are either well below or well above the ALs (Scenarios 1 and 4), then CIs may not impact project decisions. For example, if the parent concentrations at a site are all below 1 mg/kg, and the AL is 100, then likely CIs will not impact the decisions, even if they are above the project RSD or CIs goals. Similarly, parent concentrations at 100 mg/kg compared to an AL of 1 mg/kg render CIs less important in terms of decision-making.
- When parent concentrations are near the AL, and the uncertainty overlaps the decision threshold (Scenarios 2 and 3), CIs become an important factor in determining confidence in decision-making. In this case, evaluation of CIs is critical in terms of overall data usability.
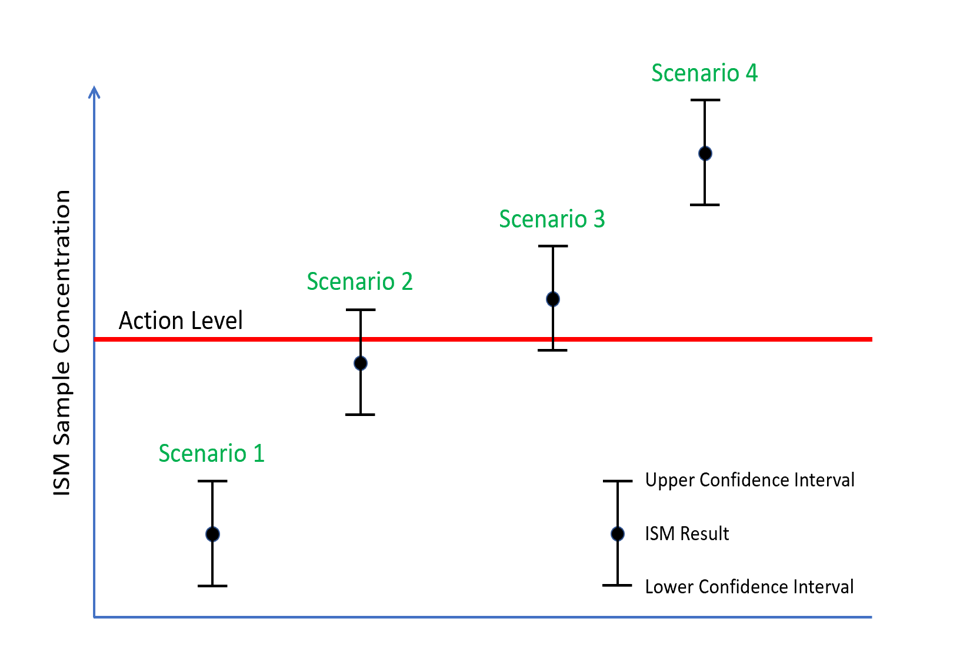
Source: Jason Brodersen, Tetra Tech, Inc., 2019. Used with Permission.
CIs are valuable when use of the parent value alone is not acceptable or desired. While there are several CI types, the 95% UCL of the replicate mean is the most common. CIs can be applied to a single DU with its own replicates, or the CV from those replicates can be applied to nearby or relevant DU concentrations within the project to derive CIs for DUs without replicates (see Section 3.3.1). Parent results with applied CIs can be applied to any of the detailed evaluation types identified above. Use of CIs is a project-by-project evaluation and should be considered thoroughly during planning phases. Some agencies require CIs, some do not – as a result, the evaluation of parent concentrations without CIs may be acceptable, given project DQOs.
6.4.3 Step 3: limitations of replicate results and sampling methodology
If the replicate results do not meet the project objectives, or if replicate results do not provide enough confidence to make site decisions as discussed in Section 6.4.2, then the project team must plan for alternatives that may include changing the initial ISM sampling design utilized – for example, if the DUs were too large, not enough increments were collected, or a larger sample mass is needed.
Regardless of the investigation objectives, it is important to review the replicate results and other factors that might contribute to confidence in the data (such as final number of increments or if the mass was obtained as intended) while making conclusions and findings.
6.4.4 Next steps
Use the results from the three previous steps to determine if the DQOs were met or if they can be optimized by additional ISM investigations. If the DQOs are not met, the methodology may be optimized in several manners, such as collecting more soil mass, collecting more increments, adding analytes to a DU, splitting a DU into multiple DUs, or adding new DUs.
Click Here to download the entire document.